コラム・調査レポート
2025.10.23
コラム
状態空間モデルとPOSデータ分析
■ 前書き
POSデータを利用すれば、「特定のメーカーの特定の商品の売上の日次推移」といった細かい粒度のデータを入手できる。特に、日経POSでは、ジャンル、サイズ別に詳細なカテゴリで分類されており、様々な分析に対応することができると評価いただいている。
POS データにおける時系列の推移は典型的な時系列分析としてモデリングすることができる。しかし、解釈性が高い手法を適切に選択することは簡単ではない。分析の目的によっては結果の解釈が難しく、有益な示唆が期待できるとはいえない。LSTMやTransformerなどの深層学習の手法を用いることも多いが、結果の解釈が難しい。ARIMAなどのモデルもよく利用されるが、外部変数を考慮するなどの分析者のドメイン知識を明示的に考慮した柔軟なモデリングをすることは難しい。
そこで、本稿では、結果の解釈がしやすく、分析者のドメイン知識を入れやすい状態空間モデルを紹介する。はじめに状態空間モデルの概念とその手法、利点について説明する。次に簡単な状態空間モデルでPythonのコード例とともに、実際の日経POSデータを用いて、気温の売り上げへの影響の経時的変化の分析において有益な示唆を得られる例を示す。最後に実装上の注意点など、発展的な分析の足がかりとなる情報を示す。
■ 状態空間モデルと、その利点
状態空間モデルは、直接観測できる値に加えて、観測できない「状態」という変数を導入したモデルである。状態空間モデルが柔軟で解釈しやすいモデルである理由としては、主に2つある。1つは確率モデルであること、もう1つは、分析者が分析要件に適していると想定している変数を、観測できない「状態」として柔軟に導入できることである。
まず「確率モデル」とはどのようなものかについて説明する。確率モデルは、不確かさを扱うためのモデルである。確率モデルでは、「観測値は値そのものではなく、ある確率分布から得られた標本である」と捉える。単一の値そのものだけではなく、蓋然性、すなわち「おおよそどの範囲にどの程度の確率で値が位置するか」といった不確実性に関する情報をも同時に記述することが可能となる。
次に「状態」の柔軟な導入について述べる。状態空間モデルは制御工学の領域で盛んに議論されてきた [1]。例えば人工衛星の軌道推定においては、センサーから得られる位置情報には観測ノイズが含まれる。このとき、状態空間モデルを用いることで、直接観測できない真の衛星の位置や速度といった「状態」を、不確実性を明示的に考慮しながら推定することが可能となる [2]。この物理的な例は、ノイズを含む観測値から背後にある状態を推定するという状態空間モデルの基本的な役割を直感的に理解する助けとなる。さらに、この枠組みは経済学の領域にも応用されている。たとえば GDP(国内総生産)のような観測可能な経済指標を出発点として、直接には観測できない「景気の良し悪し」といった潜在的な状態を推定することができる [3]。この場合の「状態」は、トレンドや景気循環、さらには季節性など、分析者が重要と考える複数の要素を含めることができるため、モデルの解釈性を保ちながら柔軟な設計が可能である [4]。
このように、物理的な現象の推定問題から経済時系列の分析まで、状態空間モデルは「ノイズを含む観測値から潜在的な状態を推定する」という統一的な枠組みを提供している。「状態」の他の事例については [4] の第9章を参照されたい。
では、この「状態」はどのように数理的に表現されるのだろうか。先ほども述べたように、状態空間モデルでは、ARIMAモデルのように実際に観測される値同士を直接モデリングするのではなく、「状態」を挟んで間接的にモデリングする。
状態と観測値の関係を図で書くと以下のようになる。
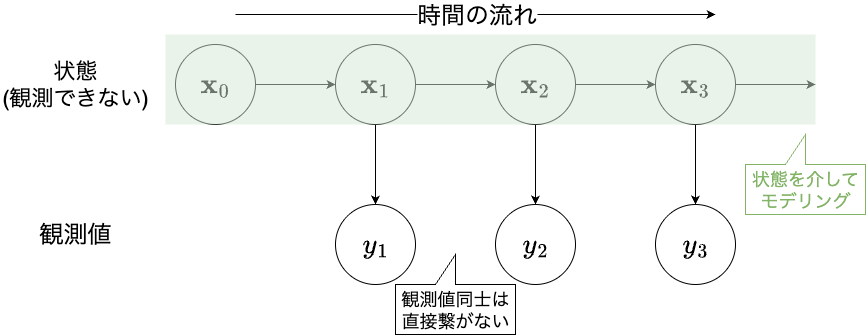
この図は、時点tにおける観測値y_tはその時点の状態の値x_tのみから決まり、時点tにおける状態の値x_tはその1期前の状態の値x_{t-1}のみから決まる、ということを表している。各時点の観測値はそのときの状態の値から決まり、前の観測値から直接条件づけられるものではない。
そして、この「y_tとx_tの関係」、「x_tとx_{t-1}の関係」の2つが「線形」かつ「ガウシアン(正規分布)」で決まるモデルを「線形ガウス型状態空間モデル」と呼ぶ。数式で表すと以下のようになる。ここで、x_tは各時点の状態、y_tは各時点の観測値、G_tは状態遷移行列、F_tは観測行列である。w_t, v_tは互いに独立な正規分布に従うノイズを表す。
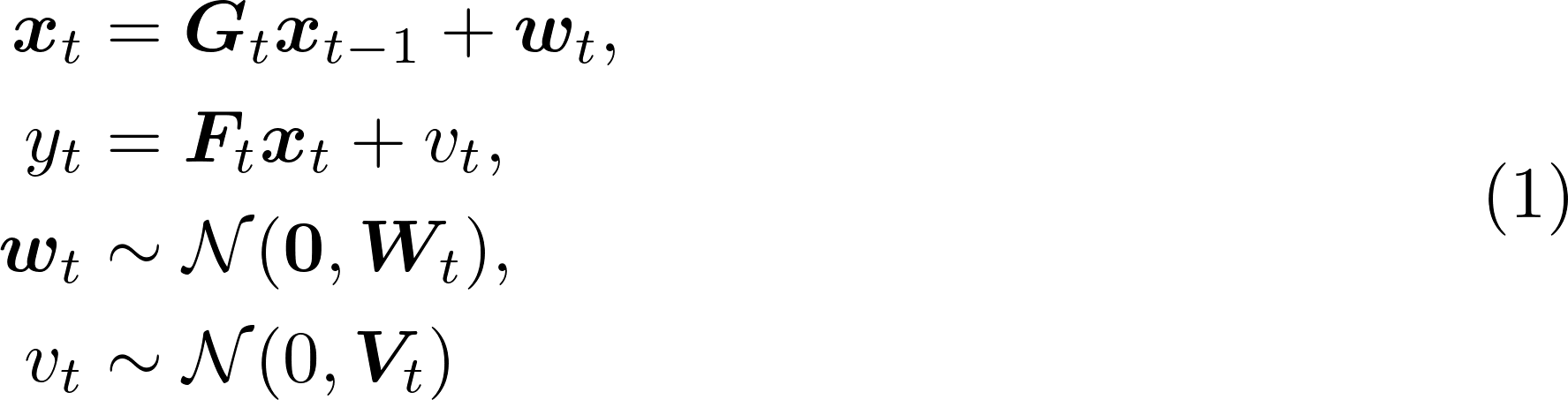
ある時点までの観測値で条件づけたその時点での「状態」の確率分布を導出する処理は、フィルタリングと呼ばれている。特に「線形」かつ「ガウシアン」を仮定する状態空間モデルが良く用いられる。これは他の仮定を置いた場合と比べて効率的なアルゴリズム(カルマンフィルタ[4,5])が存在するためである。
■ 状態空間モデルを用いた実際の分析例
日経POSデータを用いた実際の分析例を紹介する。状態空間モデルは柔軟にモデルを組めることが利点であるが、まずは簡単なモデルから紹介する。
今回はとあるメーカーのアイスクリームの売上額が、気温の変化によってどのように変化するかに着目する。期間は2025年3月から5月までとして、気象庁が公開する東京の気温データ[6]と、日経POSデータから取得できる「千人あたり金額」のデータとの関連性を調べていく。
もし時系列データでないなら、まずは以下のような単純な回帰分析を考えるであろう。
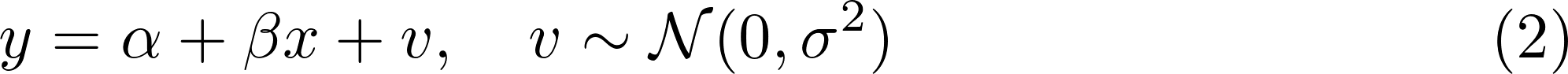
ここで、yは目的変数(今回は売上(千人あたり金額)を表す)、xは説明変数(今回は気温)、αは回帰切片、βは回帰係数、vは誤差項である。βの値を見れば、気温の高さと売上の関係性がわかる。
しかし、このままでは、時間による変化を捉えることができない。例えば、気温が高くなると気温の売上への影響も大きくなってくるかもしれないし、その傾向も時期によって変化しているかもしれない。
そこで、係数が時間で変化するモデルを考える[4]。これは、数式にすると以下のようになる。
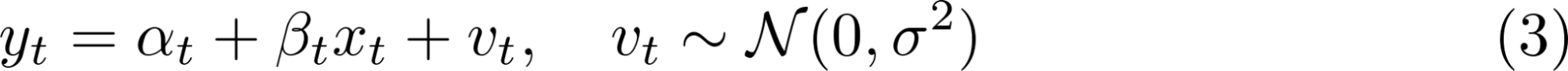
これは、実は式(1)の状態空間モデルとして表すことができる。式(1)と比べると以下の式(4)のようになる。つまり、「状態」を、「切片と回帰係数」としてモデリングしている。ここで、Iは単位行列である。
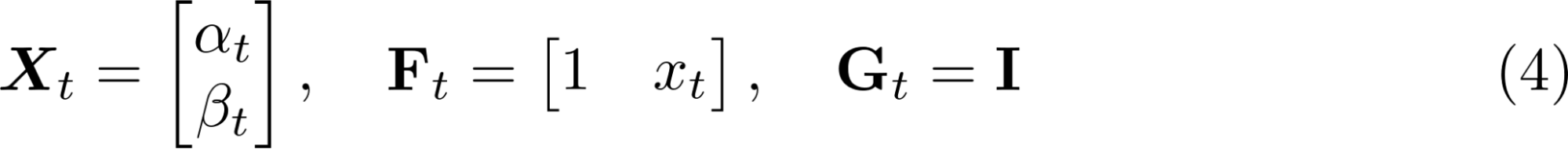
このような時間で変化し、かつ解釈しやすい回帰係数を考えることは、ARIMAモデルや深層学習のモデルでは簡単ではない。
この状態空間モデルを使って、あるメーカーのアイスクリームの「千人あたりの金額」データから示唆を得るPythonでのコード例を以下に示す。線形ガウス型状態空間モデルは、statsmodelsというライブラリが利用することができる。以下は、PandasのDataFrameに格納されたPOSデータである。
df.head(5)| 日 | 千人あたり金額 | 平均気温 |
|---|---|---|
| 2025-03-02 | 3.6 | 14.6 |
| 2025-03-03 | 0.8 | 5.9 |
| 2025-03-04 | 2.4 | 2.4 |
| 2025-03-05 | 3.0 | 5.3 |
| 2025-03-06 | 2.6 | 9.1 |
以下は、モデルを作成してフィッティングするコードである。
コード例1
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import norm
from statsmodels.tsa.statespace.sarimax import SARIMAX
def fit_regression_statespace_to(
df: pd.DataFrame,
*,
endog_column_name: str = "千人当り金額",
exog_column_names: list[str],
):
"""
状態空間モデルを用いて外生変数付き回帰を推定する。
パラメータ
----------
df : pandas.DataFrame
時系列データを格納した DataFrame。
endog_column_name : str, default="千人当り金額"
目的変数(従属変数)の列名。
この列がモデルの観測系列 (endog) として利用される。
exog_column_names : list of str
説明変数(外生変数)の列名リスト。
少なくとも1つ指定する必要がある。
戻り値
------
result : statsmodels.tsa.statespace.sarimax.SARIMAXResultsWrapper
推定結果のオブジェクト。
"""
if not exog_column_names:
raise ValueError("説明変数を少なくとも1つ指定してください")
y = df[endog_column_name]
X = df[exog_column_names].copy()
X["const"] = 1.0 # 切片を時変の状態として入れるなら、必要
model = SARIMAX(
endog=y,
exog=X,
order=(0, 0, 0),
time_varying_regression=True,
mle_regression=False,
)
result = model.fit(method="lbfgs", maxiter=500, disp=False)
return result
result = fit_regression_statespace_to(df, exog_column_names=["気温"])
result.model.ssm.transition # 状態遷移行列
result.model.ssm.design # 観測行列
model.fit()は、式(1)におけるパラメータの推定してフィルタリングも行ってくれる。式(1)がどのようにモデリングされたかは、model.fit() の返り値 result を用いて確認できる。result.model.ssm は KalmanFilter クラス [7] のインスタンスであり、その属性である transition や design により状態遷移行列と観測行列を確認できる、という仕組みになっている。
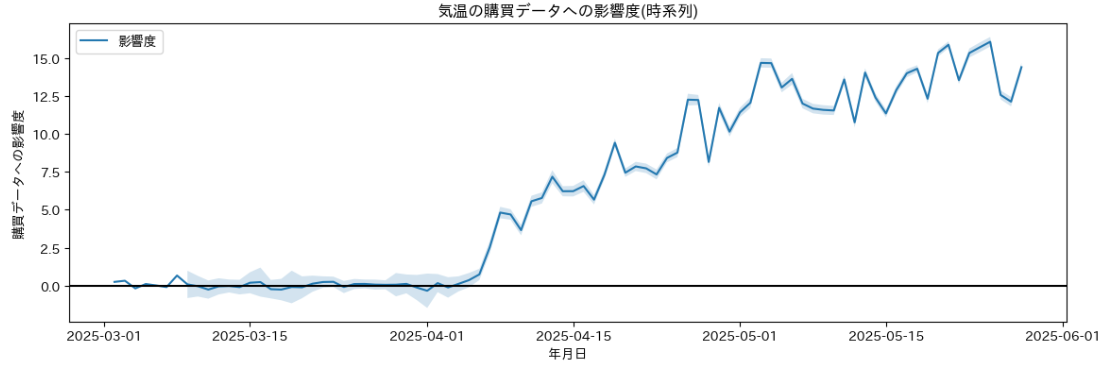
続いて、ここからフィルタリングで推定された、回帰係数の時系列推移を図示する。ここでは、回帰係数β_tは、時点tにおける気温のアイスへの売り上げへの影響度である。薄く塗ってある領域は、95%信用区間を表す(ただし最初の7日間は省略した。信用区間が大きく視認性を損ねるためである。)。95%信用区間とは、この範囲に95%の確率で値が存在すると推定していることを表す。このように、単独の値だけでなく推定される区間が出せることも状態空間モデルの利点である。
コード例2
def plot_timevarying_regression_coefficient_with_confidence(
fitted_result,
time_series_index,
ci_skip: int = 0,
const_column_name="const",
):
"""
回帰係数ごとに別のグラフで
推定された値と信頼区間の時系列を描画する
Parameters
----------
fitted_result : statsmodels 結果オブジェクト
time_series_index : array-like
x軸に使うインデックス(日付など)
ci_skip : int, optional
信頼区間の描画をスキップする先頭の期間数(期間の初期は不安定なので) (今回のグラフの出力では7)
"""
state_names = [name.removeprefix("beta.") for name in fitted_result.model.state_names]
coefs = fitted_result.filtered_state
coef_se = np.sqrt(fitted_result.filtered_state_cov.diagonal(axis1=0, axis2=1)) # 各状態の分散を導出するため、状態の共分散行列の対角成分を取得
coef_df = pd.DataFrame(coefs.T, index=time_series_index, columns=state_names)
low95 = coef_df - norm.ppf(0.975) * coef_se
up95 = coef_df + norm.ppf(0.975) * coef_se
fig, axes = plt.subplots(
len(state_names), 1, figsize=(12, 4 * len(state_names)), sharex=False
)
if len(state_names) == 1:
axes = [axes]
for ax, name in zip(axes, state_names):
ax.plot(coef_df.index, coef_df[name], label="影響度")
ax.fill_between(coef_df.index[ci_skip:], low95[name].iloc[ci_skip:], up95[name].iloc[ci_skip:], alpha=0.2)
ax.axhline(0, color="k")
ax.set_xlabel("年月日")
ax.set_ylabel("購買データへの影響度")
ax.set_title(f"{name}の購買データへの影響度(時系列)")
ax.legend(loc="upper left")
plt.tight_layout()
plt.show()
plot_timevarying_regression_coefficient_with_confidence(fitted_result, data.get_column("日").to_pandas(), ci_skip=7) # 最初7日間の分散が大きいため除く
ここから、4月になり気温が高くなってから、「1℃上がることによる売り上げへの影響」が徐々に大きくなっている、ということが示唆される。つまり、気温が高くなると、気温の変化に対して売上が大きく反応するようになる、ということである。提案されるマーケティング戦略としては、4月頃になったら気温に応じて在庫を多めに確保する、広告配信において4月になったら暑さを実感しやすい時間帯やエリアに集中投下する、などの戦略が考えられる。
■ Pythonコードの実装について
- ● 今回は、statsmodelsのSARIMAXクラスを利用して実装している。statsmodelsは、トレンドや季節成分を組み込んだ状態空間モデルとしてUnobservedComponentsを提供しており、Pythonを用いた実装の解説では一番よく用いられる。しかし、今回は回帰係数が時間で変化するモデル化を行うため、statsmodels.tsa.statespace.sarimax.SARIMAX を用いた。
- ● statsmodelsの状態空間モデルは、収束が悪い時warningが出る。収束が悪い時は、start_params引数などを通して調整を行うこともある。詳しくは[8]などを参照。
- ● 今回、SARIMAX の order引数は (0, 0, 0) とした。デフォルトでは (1, 0, 0) となっている [9]が、このままでは状態空間表現における状態遷移行列が本来意図したものではない。orderの第一要素は自己回帰次数(AR成分)を表しており、デフォルトのままでは AR(1) が導入される。その結果、式 (1) における状態ベクトル x_tに、直前の観測値 y_{t-1}に依存する成分が含まれてしまう。
■ まとめ
本稿は、状態空間モデルの紹介と、それをPOSデータに適用した簡単な実例を示した。
実際は影響度の推移を推定したい変数として、気温データの他、検索エンジンにおけるトレンドキーワード指数、メーカーのキャンペーンなど多くの時変の変数を組み込み、より複雑な分析に発展することができる。また、曜日や季節などの周期的要因、祝日の効果、全体的なトレンド(上昇・下降傾向)といった特徴を加えることで、複数の要因が同時に影響する実際の売上構造を近似するモデルを構築することもできる[10]。たとえば「週末に強い季節商品」や「祝日に需要が高まる商品」といったパターンを同時に捉えられるようになり、より現実的かつ解釈力のあるモデルとすることができる。
- [1] R. E. Kalman, “A new approach to linear filtering and prediction problems,” Journal of Basic Engineering, vol. 82, no. 1, pp. 35–45, Mar. 1960.
- [2] L. A. McGee, Discovery of the Kalman Filter as Practical Tool for Aerospace and Industry, NASA Tech. Paper 2451, 1985.
- [3] J. H. Stock and M. W. Watson, “New indexes of coincident and leading economic indicators,” NBER Macroeconomics Annual, vol. 4, pp. 351–394, 1989.
- [4] 萩原淳一郎,瓜生真也,牧山幸史,『基礎からわかる時系列分析―Rで実践するカルマンフィルタ・MCMC・粒子フィルタ―』, 技術評論社, 2021.
- [5] 野村 俊一, 『カルマンフィルタ―Rを使った時系列予測と状態空間モデル―』, 共立出版, 2016.
- [6] 気象庁「過去の気象データ検索(日ごとの値:気温)」
(https://www.data.jma.go.jp/stats/etrn/index.php) 2025年8月25日閲覧 - [7] Statsmodels. “KalmanFilter” Statsmodels Documentation
https://www.statsmodels.org/dev/generated/statsmodels.tsa.statespace.kalman_filter.KalmanFilter.html - [8] 馬場真哉. “Pythonによる状態空間モデル.” Logics of Blue, 2017年5月30日(最終更新:2017年6月6日)
https://logics-of-blue.com/python-state-space-models/ - [9] Statsmodels. “SARIMAXModel” Statsmodels Documentation
https://www.statsmodels.org/dev/generated/statsmodels.tsa.statespace.sarimax.SARIMAX.html - [10] 樋口 知之, 『予測にいかす統計モデリングの基本 改訂第2版 ベイズ統計入門から応用まで (KS理工学専門書)』, 講談社, 2022.